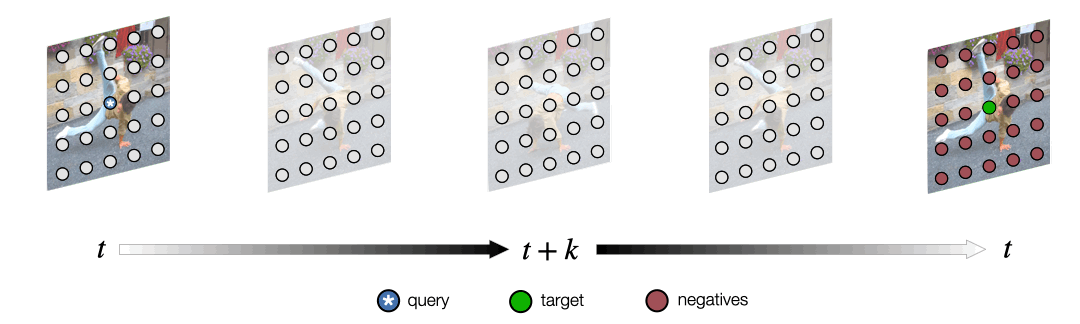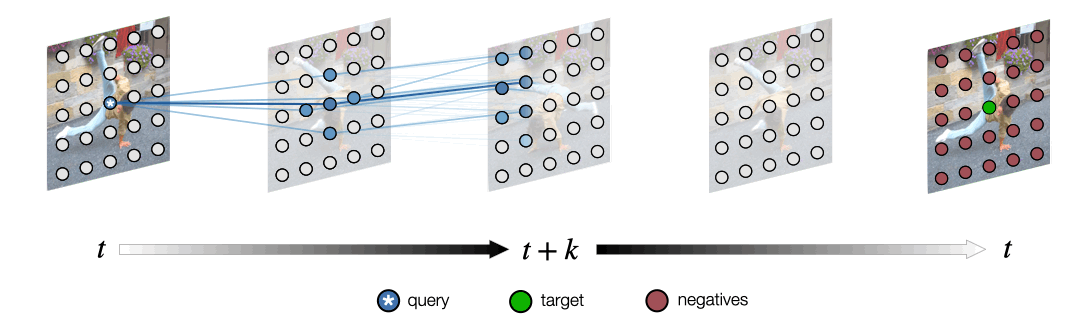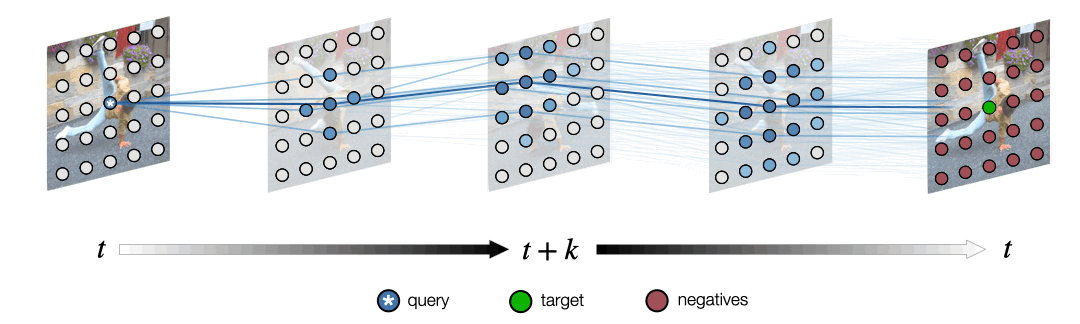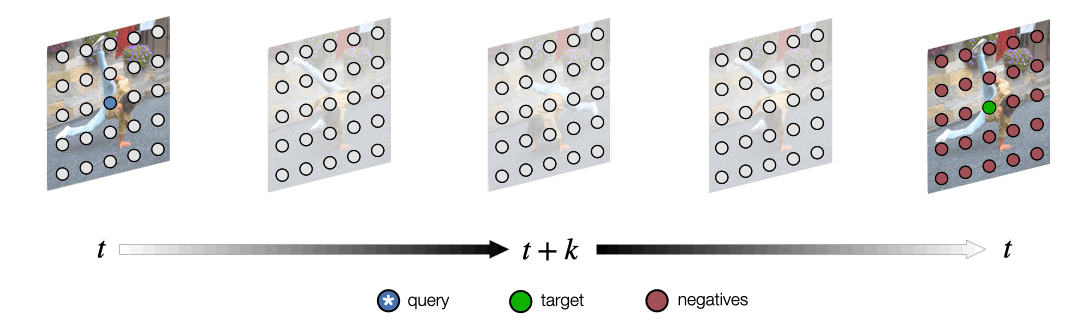
Acknowledgements
We thank Amir Zamir, Ashish Kumar, Tim Brooks, Bill Peebles, Dave Epstein,
Armand Joulin, and Jitendra Malik for very helpful feedback. We are also grateful to the wonderful
members of VGG for hosting us during a dreamy semester at Oxford. This work would not
have been possible without the hospitality of Port Meadow and the swimming pool on Iffley Road.
Research was supported, in part, by NSF grant IIS-1633310, the DARPA MCS program, and NSF
IIS-1522904. AJ is supported by the PD Soros Fellowship.
|